প্রচলিত ৪টি সংখ্যা পদ্ধতির মধ্যে পারস্পারিক মোট ১২ টি রুপান্তর সম্ভব। তবে মাত্র ৩টি রুপান্তরের নিয়ম শিখলেই আমরা বাকি রুপান্তরগুলো করতে পারবো। তবে কি সেই ৩টি নিয়ম?
১। ডেসিমাল থেকে নন-ডেসিমাল
২। নন-ডেসিমাল থেকে ডেসিমাল
৩। নন-ডেসিমাল পারস্পারিক রুপান্তর
ডেসিমাল থেকে নন-ডেসিমাল
একটি সংখ্যার দুইটা অংশ থাকতে পারে। পূর্ণাংশ ও ভগ্নাংশ। এই দুই অংশকে পৃথক করে দশমিক বিন্দু বা রেডিক্স পয়েন্ট।
ডেসিমাল থেকে বাইনারীঃ
পূর্ণ সংখ্যার ক্ষেত্রে করণীয় ধাপগুলোঃ
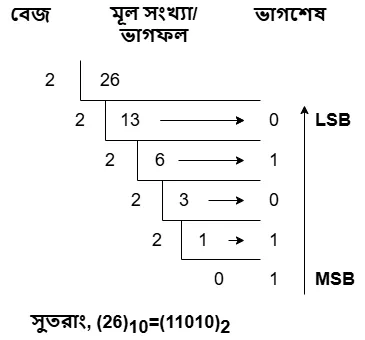
ধাপ-১ : ডেসিমাল সংখ্যটিকে টার্গেট সংখ্যা পদ্ধতির বেজ দিয়ে ভাগ করব।
ধাপ-২ : প্রাপ্ত ভাগফলকে নিচে ও ভাগশেষকে ডান পাশে লিখব।
ধাপ-৩ : ভাগফল শুন্য(০) না হওয়া পর্যন্ত উপরের ধাপগুলো চালিয়ে যাবো
এখন ডানপাশের ভাগশেষগুলোকে নিচ থেকে উপরের দিকে পর্যায়ক্রমে সাজালেই কাঙ্ক্ষিত সংখ্যা পদ্ধতিতে রুপান্তরিত মান পাওয়া যাবে।
উদাহরণঃ ডেসিমাল সংখ্যা পদ্ধতির 26 -কে বাইনারীতে রূপান্তর করো। অথবা, (26)10=(?)2
ভগ্নাংশের ক্ষেত্রে নিয়মটা ঠিক উল্টা।
ভগ্নাংশের ক্ষেত্রে করণীয় ধাপগুলোঃ
ধাপ-১ : ডেসিমাল সংখ্যার ভাগ্নাংশকে টার্গেট সংখ্যা পদ্ধতির বেজ দিয়ে গুণ করব।
ধাপ-২ : প্রাপ্ত গুণফলের পূর্ণ অংশ সংগ্রহ করে রাখবো, পূর্ণ অংশ না থাকলে ০ লিখব।
ধাপ-৩ : গুণফলের ভাগ্নাংশ শূন্য (০) না হওয়া পর্যন্ত উপরের ধাপগুলো চালিয়ে যাবো।
তবে গুণফলের ভগ্নাংশ শূন্য(০) না পেলেও ৩/৪ বার উপরের ধাপগুলো অনুসরণ করে তা আসন্ন মান হিসেবে ধরে নেওয়া যেতে পারে।
এখন পুর্ণাংশগুলিকে উপর থেকে নিচের দিকে পর্যায়ক্রমে সাজালেই কাঙ্ক্ষিত সংখ্যা পদ্ধতিতে রুপান্তরিত মান পাওয়া যাবে।
উদাহরণঃ ডেসিমাল সংখ্যা পদ্ধতির .32 -কে বাইনারীতে রূপান্তর করো। অথবা, (.32)10=(?)2
এই একই নিয়ম মেনে ডেসিমাল থেকে অন্যান্য সকল সংখ্যা পদ্ধতিতে রুপান্তর করা যাবে।
ডেসিমাল থেকে অক্টালঃ
উদাহরণঃ (283.356)10 = (?)8
ডেসিমাল থেকে হেক্সাডেসিমালঃ
উদাহরণঃ (5839.7253)10=(?)16
